Optimum Resource Allocation
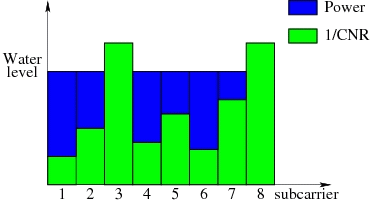
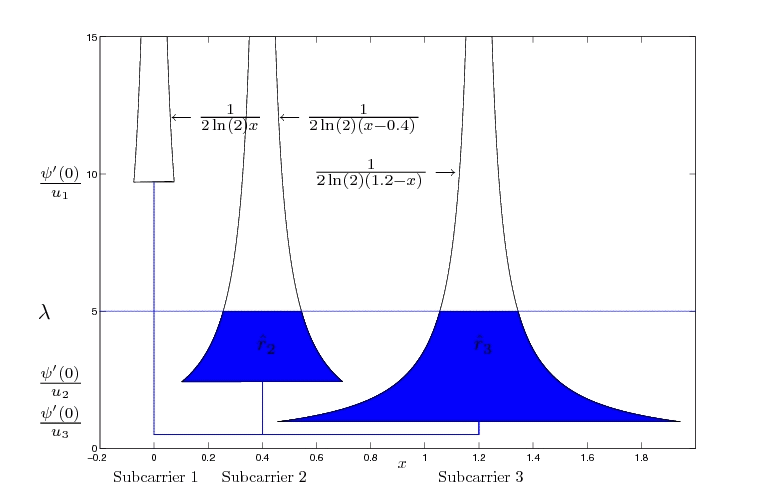
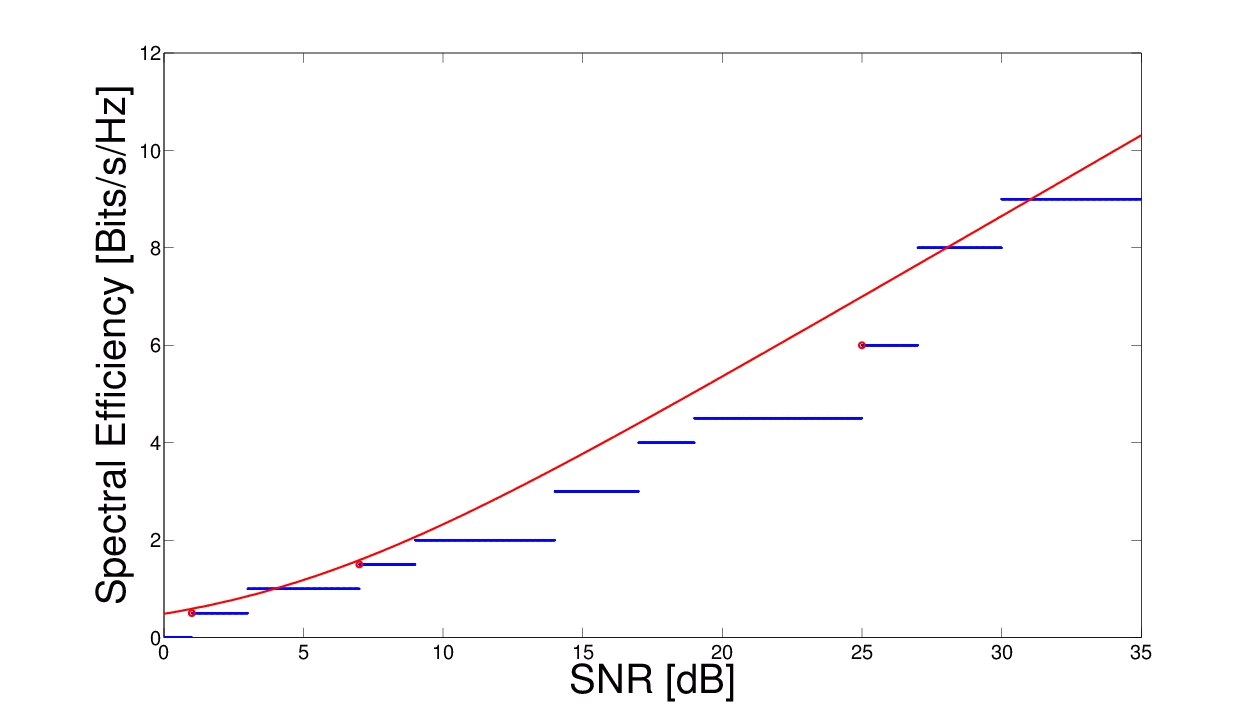
In an orthogonal frequency-division multiplexing (OFDM) system, the frequency band is split into multiple independent resource blocks that can be modeled as non-interfering flat narrowband channels. In OFDMA (OFDM Multiple Access) systems, multiple users are served simultaneously by assigning these blocks or subcarriers to users in a way that each subcarrier is occupied by at most one user. Adaptive coding and modulation techniques allow users to adapt their data transmission scheme to the wireless channel conditions on a per-subcarrier basis, maximizing frequency diversity gain. Energy efficiency and high data rates are important design principles for future wireless systems based on OFDMA. Consequently, there are basically the following aproaches:
- Rate adaptive (RA) optimization, which maximizes the overall rate given a fixed power budget.
- Margin adaptive (MA) optimization, where the transmitted power is minimized while fulfilling certain user rate demands.
- A mixture of RA and MA optimization.
The combinatorial nature of these problems is computationally prohibitive, such that the development of approximation techniques and algorithms plays an important practical role. However, by combining results from integer, convex, and nonconvex optimization theory, performance estimates and bounds for these approaches can be derived.
As intermediate step the discrete rate-power step function is often approximated by a continuous convex function in order to apply algorithms from convex optimization for efficient evaluation.
The resource allocation algorithms usually rely on the fact that a feasible solution exists. Hence, admission control on one hand should ensure that the resource allocation is able to find a solution and on the other hand should refuse as few users as possible. Altogether admission control is a challenging task, particularly, as it should take into account the nearby future.
Related research topics and publications
Rate adaptive optimization
- C. Liu, P. Wang, A. Schmeink, R. Mathar, Joint BS Selection and Subcarrier Assignment for Multicell Heterogeneous OFDM Unicasting, Proceedings: IEEE International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC), Toronto, Canada, September 2011.
- S. Görtzen, A. Schmeink, A theoretical framework for capacity-achieving multi-user waterfilling in OFDMA, Proceedings: IEEE International Symposium on Information Theory and its Applications (ISITA), Taichung, Taiwan, October 2010.
- S. Görtzen, A. Schmeink, Visualization and analysis of the OFDMA downlink capacity region, Proceedings: International OFDM-Workshop (InOWo), Hamburg, September 2009.
- C. Liu, A. Schmeink, R. Mathar, Efficient Power Allocation for OFDM with Imperfect Channel State Information, Proceedings: IEEE WiCOM 2009, Beijing, China, September 2009.
- C. Liu, D. Bielefeld, R. Mathar, Optimal Rate and Power Allocation for OFDM in the Presence of Channel Uncertainty, Proceedings: IEEE PIMRC, Cannes, France, September 2008.
- R. Mathar, M. Reyer, Iterated Water-Filling for OFDMA Rate and Power Allocation with Proportionality Constraints, Proceedings: IEEE GLOBECOM 2007, Washington, November 2007.
Margin adaptive optimization
- S. Görtzen, A. Schmeink, Optimality of Dual Methods for Discrete Multiuser Multicarrier Resource Allocation Problems, IEEE Transactions on Wireless Communications, vol. 11, no. 10, pp. 3810-3817, October 2012.
- C. Liu, L. Schiefler, A. Schmeink, R. Mathar, Energy Efficiency on Real Time Transmission in Multiuser OFDM Downlink, Proceedings: IEEE SPAWC 2011, San Francisco, June 2011.
- C. Liu, A. Schmeink, R. Mathar, Constant-Rate Power Allocation under Constraint on Average BER in Adaptive OFDM Systems, Proceedings: IEEE International Conference on Communications (ICC 2010), Cape Town, South Africa,, May 2010.
- C. Liu, A. Schmeink, R. Mathar, Power Allocation for Broadcasting in Multiuser OFDM Systems with Sublinear Complexity, Proceedings: IEEE ICC, Dresden, June 2009.
- C. Liu, G. Böcherer, R. Mathar, Accelerating Resource Allocation for OFDMA Downlink with CNR Variation Over Users, Proceedings: IEEE VTC Spring 2009, Barcelona, April 2009.
- C. Liu, R. Mathar, Optimal and Efficient Bit Loading for OFDM in the Presence of Channel Uncertainty, Proceedings: IEEE ISWCS, Reykjavik, Iceland, October 2008.
- C. Liu, R. Mathar, M. Reyer, Fast Resource Allocation for OFDMA Downlink Utilizing An Efficient Discrete Bit Loading, Proceedings: IEEE WiCOM, Dalian, China, October 2008.
- C. Liu, D. Bielefeld, R. Mathar, Optimal Rate and Power Allocation for OFDM in the Presence of Channel Uncertainty, Proceedings: IEEE PIMRC, Cannes, France, September 2008.
- C. Liu, R. Mathar, Fast and Efficient Power and Rate Allocation for Multiuser OFDM Downlinks, Proceedings: IEEE PIMRC, Cannes, France, September 2008.
- A. Feiten, R. Mathar, M. Reyer, Rate and Power Allocation for Multiuser OFDM: An Effective Heuristic Verified by Branch-and-Bound, IEEE Transactions on Wireless Communications, vol. 7, no. 1, pp. 60-64 , 2008.
- R. Mathar, M. Reyer, Iterated Water-Filling for OFDMA Rate and Power Allocation with Proportionality Constraints, Proceedings: IEEE GLOBECOM 2007, Washington, November 2007.
Mixed margin and rate adaptive optimization
- C. Liu, A. Schmeink, R. Mathar, Dual Optimal Resource Allocation for Heterogeneous Transmission in OFDMA Systems, Proceedings: IEEE Globecom 2009, Honolulu, Hawaii, USA, December 2009.
- C. Liu, A. Schmeink, R. Mathar, A Linear-Complexity Resource Allocation Method for Heterogeneous Multiuser OFDM Downlink, Proceedings: IEEE PIMRC'09, Tokyo, Japan, September 2009.
Investigating the optimality gap if approximating the rate-power function
- M. Reyer, A. Schäper, R. Mathar, Resource Allocation in OFDM Systems -- Efficiency as Basis for Allocation and Initialization, Proceedings: International Symposium on Wireless Communication 2011, Aachen, Deutschland, November 2011.
Admission Control
- J. Gross, M. Reyer, Performance Prediction for OFDMA Systems with Dynamic Power and Subcarrier Allocation, Computer Communication, vol. 34, no. 8, pp. 973-984, June 2010.
Related projects
- Self Organization for 4G Multi-Tier Networks
Related student work
- Diploma thesis Resource Allocation for Heterogeneous Transmission in Multicell OFDM Systems
- Diploma thesis Heuristiken für Ressourcenzuweisung in Multiuser OFDMA Systemen
- Diploma thesis Power and rate allocation for heterogeneous transmission in wireless multiuser OFDM systems
- Diploma thesis Resource Allocation in OFDM-based Cognitive Radio Systems
- Bachelor thesis Analyse und Bewertung von Approximationsfehlern bei Verwendung stetiger Ratenleistungsfunktionen
- Student assistants developed tools for evaluation by simulation
Contact
For further information contact Michael Reyer.
***
Aktuelle Informationen gemäß Art. 13 DS-GVO:
Datenschutzhinweis ***
Impressum ***

